OPINION
January/February 1997

DON'T CALL IT STRESS DROP

One of the most battle-weary parameters in seismology today is stress drop. Seismologists argue over everything about this parameter, including its name, meaning, measurement, and scaling with magnitude.

The original concept of stress drop was introduced as a static measure of final fault slip, as a fraction of fault dimension (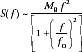), and was estimated from measurements or inferences of these geologically based parameters (as, for example, by Kanamori and Anderson, BSSA, 1975, pp. 1,073-1,095). Stress drop became an important earthquake source parameter following Brune's classic paper (JGR, 1970, pp. 4,997-5,009), showing that the radiated far-field spectrum of shear waves could be interpreted in terms of a simple point-source model with just two source parameters--seismic moment (M₀) and stress drop (). This paved the way for measurments of stress drop from seismic signals. In Brune's model, the acceleration source spectrum has a simple "omega-squared" shape,

Stress drop assumed an important role in engineering seismology when Hanks and McGuire (BSSA, 1981, pp. 2,071-2,095) showed that by combining the Brune point-source model with some basic equations from random-process theory, the salient features of high-frequency ground motion could be successfully modeled. Using a stress drop of 100 bars as a parameter by which to scale the high-frequency level of the source spectrum, they were able to match average observed rms and peak ground acceleration values for California earthquakes. Significantly, they also noted that the actual values of static stress drop were generally lower than 100 bars. Numerous subsequent studies confirmed the utility of the stochastic-model approach in interpreting strong-motion observations, and proliferated the use of stress drop as an index parameter by which to measure the strength of the observed high-frequency spectral level. As a result, stress drop has become a key predictive parameter in the development of ground-motion relations, particularly for eastern North America.

Not surprisingly, different definitions of stress drop have resulted in large discrepancies in reported stress drop values. For example, one study reported a stress drop of about 500 bars for the 1990 M 4.7 Mont Laurier, Québec earthquake, based on the average amplitude of the Fourier spectrum at high frequencies (calculation from a_hf); another study quoted a stress drop of only 25 bars for this event, based on the radius of the aftershock zone (assumed representative of r). Similarly, stress drop values for the 1988 M 5.8 Saguenay earthquake range from a low of 70 bars to a high of 600 bars. The wide range of the estimates reflects the wide range of parameters being measured and supports the view that static source characteristics are not reliable predictors of high-frequency ground motion, particularly for complex ruptures. What, then, should you infer when someone tells you a certain earthquake had a stress drop of 100 bars? Answer: absolutely nothing, until you learn exactly what was measured and how.

The original definition of static stress drop as a measure of slip relative to fault dimension is clear and has a direct physical meaning. Unfortunately, this definition has limited practical utility; with the exception of large well documented earthquakes, it is difficult to measure slip and fault dimensions.

Our subsequent attempts to recast stress drop in terms of easily measured seismological parameters like corner frequency, source duration, or spectral amplitudes have led to the present ambiguity and nonuniqueness in definition. The roots of this confusion lie in the assumptions that are required to associate a finite source dimension or rupture duration with a point-source representation of the far-field radiation. This association is nonunique, and many of the definitions relating quantities such as corner frequency, source duration, and fault radius involve constants that are, in reality, mere conventions. This nonuniqueness can be readily understood intuitively by considering the potential pitfalls of equating a complex finite rupture with an "equivalent" point-source.

The non-uniqueness can also be formally demonstrated by deriving the form of the Brune model from the theoretical expression for the far-field shear-wave displacement from a point dislocation in an elastic space (Beresnev and Atkinson, BSSA, Feb. 1997): in any formula relating corner frequency to source dimension (duration), the coefficient of proportionality is intrinsically ambiguous, depending on adopted conventions concerning the source time function. It follows that there is no unique relationship between stress drop and corner frequency.

In spite of all of the above, it appears from the bulk of the literature that the simple "omega-squared" spectrum implied by the Brune point-source model describes small, simple ruptures reasonably well and is a surprisingly good approximation for many large events. This might imply that the relative slips on simple faults are not highly variable. But for complex ruptures, or for large events for which finite-fault effects are significant, deviations from this simple representation become important. These deviations can be modeled using a variety of concepts, including fractional stress drop, variable slip, dominant asperities or barriers, strong directivity effects, etc. In these cases the spectrum becomes complicated and stress drop becomes a highly ambiguous and nonunique parameter, depending entirely on how it is measured.

All this begs the question of whether we really need to use stress drop as a descriptive source parameter for engineering seismology. Its main utility in recent years has been as a measure of the strength of the high-frequency radiation, particularly in the development of stochastic ground motion relations. It is convenient to have some parameter to express this spectral level, but should it be called stress drop?

We suggest a more direct alternative for the description and modeling of ground motion amplitudes. There is widespread consensus that, on average, "well-behaved" earthquakes--fairly simple ruptures with source spectra not too different from the omega-squared shape--have Brune stress drops within about a factor of two of 100 bars, throughout North America. (The implication is that relative slips on faults cluster around a value of 0.0003, for an assumed shear wave velocity of 3.7 km/s and density of 2.8 g/cm³.) For this situation m = M, where m is the high-frequency magnitude and M is moment magnitude (Atkinson and Hanks, BSSA, 1995, 825-833). By definition, m = 2loga_hf + 3, where a_hf is the high-frequency level of the Fourier amplitude spectrum of acceleration in cm/sec (average or random horizontal component) at a hypocentral or closest fault distance of 10 km. The relative strength of the high-frequency radiation is directly measured by the difference between the high-frequency and moment magnitudes, which we can refer to as M (i.e., M = m - M). Earthquakes with "typical" high-frequency spectral amplitudes, then, are described as having M = 0, with loga_hf = (M - 3)/2. If M = 0.6, it means that the high-frequency spectral level is twice the amplitude expected for our reference case of m = M. M can be easily determined for earthquakes throughout North America from m and M, as obtained from spectral data, peak ground velocity or felt area. By using "M-drop" in place of stress drop as a description of the strength of the high-frequency radiation observed in past earthquakes and as a predictive parameter in ground-motion models, we can avoid the confusion and misinterpretations that have arisen from the use of stress drop in this context.

For spectra that follow a simple omega-squared shape, the Brune model can be expressed in terms of M through the implied relationship between M and f₀. From the definitions above, it follows that logf₀ = 0.25 M - 0.5M - 8.78 - 0.5logC, where C is the constant of proportionality in the Brune model (i.e., a_hf = CM₀f₀²). Note, however, that M cannot be measured from f₀ or source duration, since the high-frequency level is only related to a corner frequency or duration parameter for the idealized simple model. If we want to know M we need to determine the high-frequency spectral level, using the Fourier spectrum of ground acceleration, the peak ground velocity, or the felt area.

In summary, it has been a convenient and useful practice in engineering seismology to link the radiation from real earthquakes having finite size and complex ruptures to the parameters of an "equivalent" omega-squared point-source model. Unfortunately, this link is intrinsically ambiguous, and the introduction of stress drop as a stand-in for fault dimension in making this link complicates matters further. Stress drop introduced in this manner may bear no relationship to stresses in the real Earth or on the fault surface, particularly for complex ruptures. We suggest that a direct measure of the strength of the high-frequency seismic radiation relative to the moment, M, be used as an alternative to in describing ground motions. To avoid confusion, the term stress drop should, in the future, be reserved exclusively for its earlier definition as a measure of fault slip divided by fault dimension.

Gail M. Atkinson and Igor Beresnev
Department of Earth Sciences
Carleton University
1125 Colonel By Drive
Ottawa, Ont. K1S 5B6

To send a letter to the editor regarding this opinion or to write your own opinion, contact Editor John Ebel by email or telephone him at (617) 552-8300.

Posted: 18 January 1999